Warning: This is a pretty technical and intended to be background for the next post. Read on only if you want to learn about mechanics. It will help to have at least a high school education in physics.
Since Apple’s introduction of momentum, friction, and bouncing in iOS, physical calculations have never been more relevant. In classical mechanics, a body that behaves this way is referred to mass-spring-damper system. If we want to create an element in our apps that animates and responds in a physical way, we have to understand the way these systems are modeled.
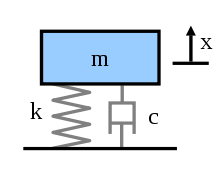
These motion of our system is dependent on three things:
The inertial effects are dependent on the acceleration and the mass (m) of the body,
The damping effect is based on the velocity of the body and some damping constant (c) (also referred to as _b _in some texts).
The bouncing effect of the spring is dependent on its displacement and the spring constant (k)
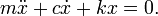
So, this is a fully second-order system, and requires hardcore differential equations to solve.
In a high school physics education, you might learn about inertial effects and forces from springs, but most likely not about dampers. A damper is, at its most high level, just a Newtonian fluid: it resists motion. The force that it imparts on the body is stronger when it is moving faster. It’s often modeled a dashpot, which you might be more familiar with as the rod that slows a screen door down. You can also imagine trying to move your hand in the pool: the faster your try to move your hand, the more strongly the water resists your motion, whereas moving slowly through the water is very easy.
The value of c can represent 4 states:
Over-damped: In this case, the damping effect is so strong that it doesn’t allow any oscillation (bouncing), before returning to its original position.
Critically damped: This is the lowest value of c that has no oscillation.
Underdamped: The damping is not strong enough, and the system overshoots and bounces while it returns to its original state. This is what we’re after.
No damping: The system doesn’t slow down at all and bounces forever.
Whether c represents an over-, under-, or critically damped system depends also on m and k.
A full derivation of our differential equation is unfortunately beyond the scope of this post. Rest assured that it’s really great and fun and you’re totally missing out. Once we solve the system given some initial displacement, we get this equation
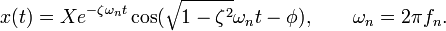
where
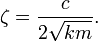
and X represents our initial displacement, and t, the time after releasing our system from its displacement. To assure that the system is underdamped, we want ς to be less than 1 but greater than 0.
The next step is to use this equation to define the motion of our animated object using a CAKeyframeAnimation, which you can read more about in the next blog post.
I used images and equations from Wikipedia. Thanks to the folks there for creating them.
