In Dave Abraham’s WWDC talk, Embracing Algorithms, he talks about finding common algorithms and extracting them into the generic (and testable) functions. One thing in this vein that I like to look for is a few collection operations that cluster together that can be combined into a single operation. Often times, when combining these operations, you’ll also find a beneficial optimization that can be drawn out.
The first example of this is a method added in Swift 3:
// when you see:
myArray.filter({ /* some test */ }).first
// you should change it to:
myArray.first(where: { /* some test */ })
The predicate block stays exactly the same and the result is the same, but it’s shorter, more semantic, and more performant, since it’s not allocating a new array and finding every single object in the array that passes the test — just the first.
Another example is the count(where:) function that I helped add to Swift 5:
// when you see:
myArray.filter({ /* some test */ }).count
// you should change it to:
myArray.count(where: { /* some test */ })
Again: shorter, more semantic, and more performant. No arrays allocated, no extra work done.
In a particular project of ours, we had one common pattern where we would do a sort followed by a prefix. This code, for example, needed to find the 20 most recently created images.
return images
.sorted(by: { $0.createdAt > $1.createdAt })
.prefix(20)
You could also imagine something like a leaderboard, where you want the top 5 users with the highest scores.
I stared at this code until my eyes began to bleed. Something was fishy about it. I started thinking about the time complexity. If you think of the length of the original array as n, and the number of items you want to end up with as m, you can start to analyze the code. The sort is O(nlogn), and prefixing is a very cheap operation, O(1). (Prefixing can be as slow as O(m), but arrays, which are what we are dealing with here, are random access collections and can prefix in constant time.)
Here’s what was bugging me: Getting the single smallest element of a sequence (using min()) requires only a single pass over the all of its contents, or O(n). Getting all of the elements ordered by size is a full sort, or O(nlogn). Getting some number m of them where m is smaller than n should be somewhere in between, and if m is much, much smaller than n, it should be even closer to O(n).
In our case, there are lots of images (n is about 55,000) and the amount we’re actually interested in small (m is 20). There should be something to optimize here. Can we optimize sorting such that will only sort the first m elements?
It turns out that, yes, we can do something along those lines. I call this function smallest(_:by:). It takes both the parameters of the sort and the prefix, which are the number m and the comparator to sort with:
func smallest(_ m: Int, by areInIncreasingOrder: (Element, Element) -> Bool) -> [Element] {
Starting with the first m elements pre-sorted (this should be quick, since m should be much smaller than the length of the sequence):
var result = self.prefix(m).sorted(by: areInIncreasingOrder)
We loop over all the remaining elements:
for element in self.dropFirst(m) {
For each element, we need to find the index of the first item that’s larger than it. Given our areInIncreasingOrder function, we can do this by passing the element first, and each element of result second.
if let insertionIndex = result.index(where: { areInIncreasingOrder(element, $0) }) {
If an index is found, that means that there’s a value bigger than element in our result array, and if we insert our new value at that value’s index, it’ll be correctly sorted:
result.insert(element, at: insertionIndex)
And remove the last element (which is now out of bounds of our number m):
result.removeLast()
If the index wasn’t found, we can ignore the value. Lastly, once the for loop is done, we can return the result:
}
}
return result
}
The whole function looks like this:
extension Sequence {
func smallest(_ m: Int, by areInIncreasingOrder: (Element, Element) -> Bool) -> [Element] {
var result = self.prefix(m).sorted(by: areInIncreasingOrder)
for e in self.dropFirst(n) {
if let insertionIndex = result.index(where: { areInIncreasingOrder(e, $0) }) {
result.insert(e, at: insertionIndex)
result.removeLast()
}
}
return result
}
}
If this is reminding of you of your early coursework in computer science classes, that’s good! This algorithm is something like a selection sort. (They aren’t exactly the same, because this pre-sorts some amount, and selection sort is a mutating algorithm and this isn’t.)
The time complexity of this is a bit tougher to analyze, but we can do it. The sort of the initial bit is O(mlogm). The big outer loop is O(n), and each time it loops, it calls index(where:) (O(m)) and insert(_:at:) (O(m) as well). (Insertion is O(m) because it potentially has to slide all the elements down to make space for the new element.) Therefore, the time complexity of this is O(mlogm + n * (m + m)), or O(mlogm + 2nm). Constants fall out, leaving us with O(mlogm + nm).
If m is much, much smaller than n, the m terms become more or less constant, and you end up with O(n). That’s a good improvement over our original O(nlogn)! For our original numbers of 55,000 images, that’s should be a roughly five-fold improvement.
This function that we’ve written is broadly an optimization over prefix + sort, but there are two smaller optimizations that I want to discuss here as well.
There’s one pretty low hanging fruit optimization here. We’re looking for the smallest 20 items in an array of 55,000 elements. Most (almost all!) of the elements we check are not going to be needed for our result array. If we throw in one check to see if the element we’re looking at is larger than the last element in the result array, and if it is, just skip it entirely. There’s no sense searching through the array for its insertion index if the element is larger than the last element of result.
if let last = result.last, areInIncreasingOrder(last, e) { continue }
Testing with this check enabled caused a 99.5% drop in linear searches through the result array, and the whole algorithm increased roughly 10x in speed. I want to credit to Greg Titus for pointing this optimization out to me — I would have missed it entirely.
If you want to go take another step, you can do one more (slightly harder to implement) optimization. This one relies on two facts. First, we’re using index(where:) to find the insertion in the result array; second, the result is always sorted. index(where:) is a linear operation by default, but if we’re searching through an already-sorted list, it can be tempting try and replace the linear search with a binary search. I took a crack at this.
To understand how these optimizations affected the performance of the algorithm, Nate Cook helped me become familiar with Karoy Lorentey’s Attabench tool, benchmarking each of these solutions. Because all of our complexity analysis until this point was theoretical, until we actually profile the code we’re concerned with (and ideally on the devices in question), any conclusions are just educated guesses. For example, sort generally is O(nlogn), but different algorithms handle different kinds of data differently. For example, already sorted data might be slower or faster to sort for a particular algorithm.
Attabench showed me a few things.
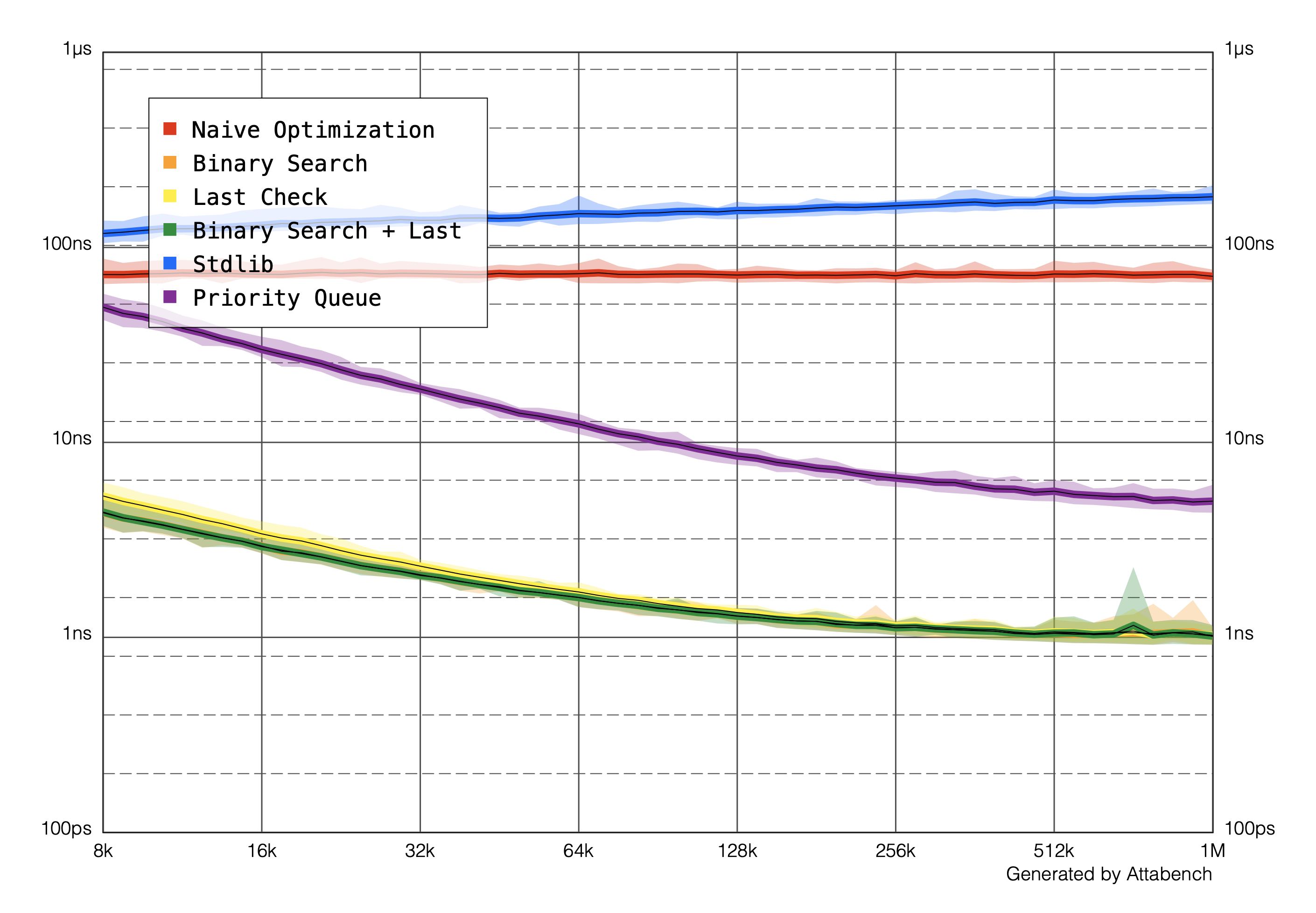
(I also threw in a priority queue/heap solution written by Tim Vermuelen, since a few people asked for how that compares.)
First, my guess that searching through the array a single time was faster than fully sorting the array was correct. Especially as the sequence in question gets long, sorting gets worse but our “naive optimization” stays constant. (The Y axis represents the time spent per item, rather than total, meaning that O(n) algorithms should be a flat line.)
Second, the “last check” and the binary search optimizations have almost exactly the same performance characteristics when they are on their own (you can’t actually see the orange and yellow lines because they’re behind the green), as when they’re used together. However, because binary search is hard to write and even harder to get right, you may decide it isn’t worth it to add.
The takeaway here for me is that profiling and optimizing is hard. While complexity analysis can seem a bit academic — “When am I going to use this in my real career?” one asks — understanding the time and space complexity of your algorithms can help you decide which directions to explore. In this case, understanding the time complexity of sorting led us towards a broad idea which bore fruit. Finally, benchmarking and profiling with a wide variety of data leads to the most accurate information about how your code will work in production.
And also, next time you see a sort followed by a prefix, think about replacing it with smallest(_: by:).
